树状数组的证明

树状数组 和 线段树 是解决区间问题常用的两种数据结构。其中线段树理解起来相对简单，而树状数组的代码实现则更简洁。

参考例题: 区域和检索-数组可修改，就是一个标准的树状数组题。更抽象的应用场景可以理解为:

1. 假设存在数组 $a_i$，
2. 存在操作 $\bigodot(a_i, a_{i+1}, a_{i+2}, \cdots, a_{i+k})$，并且

$$\bigodot(a_i, a_{i+1}, \cdots, a_{i+k}) =\bigodot( \bigodot(a_i, a_{i+1}, \cdots, a_{i+j}), \bigodot(a_{i+j+1}, a_{i+j+2}, \cdots, a_{i+k}) )\tag{1}$$

$$\bigodot(a_j, \bigodot(a_k)) = \bigodot(a_j, a_K) \tag{2}$$

3. 树状数组可以 $O(\log{}n)$ 的时间复杂度求出 $\bigodot(a_1, a_{2}, a_{3}, \cdots, a_{i})$的值。
4. 这里的 $\bigodot$ 可以是 $\sum$, 也可以是 $\prod$，或者是任意其他满足上述等式的操作。

楼主从大一就已学习树状数组，但一直断断续续的用，断断续续的忘，每次使用时都要翻出模板代码来。

最近尝试手推了一下树状数组，记录于下。

假设原数组是 $a_i$，树状数组利用 $a_i$ 构建了新数组 $b_i$。

$$b_i = \bigodot_{i-2^k+1}^{i}a_i$$

$$i \;\mathrm{mod}\; 2^k = 0 \land (\nexists{ }m > k \land i \;\mathrm{mod}\; 2^{m} = 0)$$

以 $\bigodot = \sum$ 为例，

$$b_1 = a_1 \\ b_2 = a_2 + a_1 \\ b_3 = a_3 \\ b_4 = a_4 + a_3 + a_2 + a_1 \\ b_5 = a_5 \\ b_6 = a_6 + a_5 \\ b_7 = a_7 \\ b_8 = a_8 + a_7 + a_6 + a_5 + a_4 + a_3 + a_2 + a_1 \\$$

如下图，黑色为原数组 $a_i$, 红色为数组 $b_i$

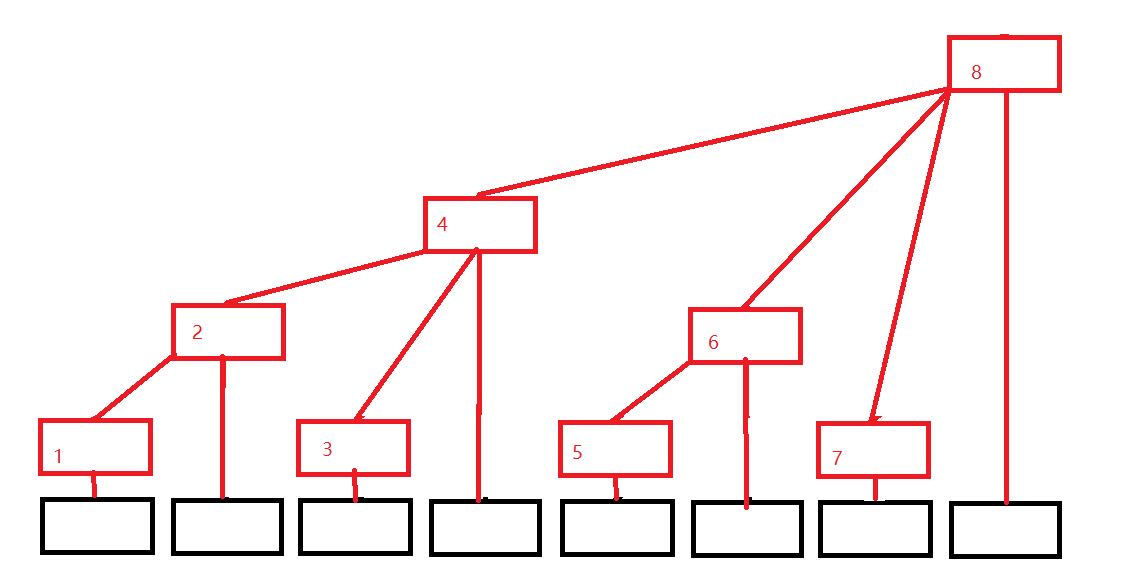
假设目标为计算 $\bigodot_{i=1}^{i=n}a_i$ 利用公式 $(1)$，可得:

$$\begin{aligned} \bigodot_{i=1}^{i=n}a_i &= \bigodot(\bigodot_{i=1}^{i=j}a_i, \bigodot_{i=j+1}^{i=n}a_i), j=2^{\lfloor log_2n \rfloor}\\ &=\bigodot(b_j, \bigodot_{i=j+1}^{i=n}a_i)\\ &=\bigodot(b_j, \bigodot(\bigodot_{i=j+1}^{i=k}a_i, \bigodot_{i=k+1}^{i=n}a_i), k=j+2^{\lfloor log_2(n-j) \rfloor}\\ &=\bigodot(b_j, \bigodot(b_k, \bigodot_{i=k+1}^{i=n}a_i))\\ &={ }\vdots\\ &=\bigodot(b_j, \bigodot(b_k, \bigodot(b_l, \cdots))), j=2^{\lfloor log_2n \rfloor}, k=j+2^{\lfloor log_2(n-j) \rfloor}, l=k+2^{\lfloor log_2(n-k) \rfloor}, \cdots\\ &=\bigodot(b_j, b_k, b_l, \cdots))), j=2^{\lfloor log_2n \rfloor}, k=j+2^{\lfloor log_2(n-j) \rfloor}, l=k+2^{\lfloor log_2(n-k) \rfloor}, \cdots \end{aligned}$$

以 $\bigodot = \sum$ 为例，

$$\sum_{i=1}^{i=1}a_i = b_1 \\ \sum_{i=1}^{i=2}a_2 = b_2 \\ \sum_{i=1}^{i=3}a_3 = b_3 + b_2 \\ \sum_{i=1}^{i=4}a_4 = b_4 \\ \sum_{i=1}^{i=5}a_5 = b_5 \\ \sum_{i=1}^{i=6}a_6 = b_6 + b_4 \\ \sum_{i=1}^{i=7}a_7 = b_7 + b_6 + b4 \\ \sum_{i=1}^{i=8}a_8 = b_8$$

所以求 $\bigodot_{i=1}^{i=n}a_i$，实际是求

$$\bigodot(b_j, b_k, b_l, \cdots))), j=2^{\lfloor log_2n \rfloor}, k=j+2^{\lfloor log_2(n-j) \rfloor}, l=k+2^{\lfloor log_2(n-k) \rfloor}, \cdots$$

对于 $i, j, k, \cdots$ 很容易通过数学公式计算出，但从位运算的角度理解更合适。 以 $n=58$ 为例，二进制转换后

$$58 = 0_b00111010$$

$$i = 0_b00100000 \\ j = 0_b00110000 \\ k = 0_b00111000 \\ l = 0_b00111010 \\$$

容易得到，$l, k, j, i, \cdots$从大到小相当于二进制消去最后的一个1.

二进制运算中，可以用 $n-(n\&{-n})$ 逐次迭代得到 $k, j, i, \cdots$。(其证明方式我已经找到了一个绝妙的方法，篇幅限制就不在这里展开了。)

树状数组不仅可以 $O(\log{}n)$ 的时间复杂度求出 $\bigodot(a_1, a_{2}, a_{3}, \cdots, a_{i})$的值。当原数组$a_i$ 更新时，仍可以 $O(\log{}n)$ 的时间复杂度更新 $b_i$。

假设 $a_i$ 更新，则只需要更新 $b_{j_1}, b_{j_2}, b_{j_3}, \cdots$的值，其中

$$j-2^k+1 \leq i \leq j$$

$$j \;\mathrm{mod}\; 2^k = 0 \land (\nexists{ }m > k \land j \;\mathrm{mod}\; 2^{m} = 0)$$

同样二进制运算的方式，用 $i + (i\&(-i)$ 逐次迭代即可得到 $j$ 序列。

下面是一个 Kotlin 实现:

class FenwickTree<T, U, R>(val size: Int, private val default: U,
                           val accumulateOp: (R, U) -> R,
                           val updateOp: (Int, T, U) -> U) {
    val tree: MutableList<U> = ArrayList<U>(size).also { tree -> (0 until size).forEach { _ -> tree.add(default) } }

    fun lowBit(index: Int) = index and (-index)

    inline fun query(index: Int, default: R): R {
        var varIndex = index
        var result = default
        while (varIndex > 0) {
            result = accumulateOp(result, tree[varIndex])
            varIndex -= lowBit(varIndex)
        }
        return result!!
    }

    inline fun update(index: Int, value: T) {
        var varIndex = index
        while (varIndex < size) {
            tree[varIndex] = updateOp(index, value, tree[varIndex])
            varIndex += lowBit(varIndex)
        }
    }
}